[모두의 딥러닝] lec 06-1. Softmax Regression: 기본 개념 소개
여러 개의 class가 있을 때 그것을 예측하는 Multinomial classification,
그 중에서도 가장 많이 사용되는 Softmax Regression에 대해서 공부할 것.
Logistic regression Review

linear한 hypothesis로 출발.
WX의 단점) RETURN 값이 실수의 값이 되어서 우리가 하려는 Binary Classification에 적합하지 않음.
--> Z라고 놓고, g(z)라는 값이 있다면 실수 값을 압축을 하여 0~1 출력값으로 나왔으면 좋겠다!
z값이 커지거나 작아지더라도 0~1에 머무는 함수가 있었으면 좋겠다!
sigmoid = logistic 함수

최종 hypothesis.
--> 간단한 그림으로 나타냄


1. 하나의 class table (W)을 계산 --> 결과값 z로 나옴
2. z값을 sigmoid라는 함수로 넣음.
3. 통과 후에 나오는 값(Y의 hat)은 0과 1 사이가 될 것이다.
(Y = 실제 값 / Y의 hat = 예측 값(= H(x)))
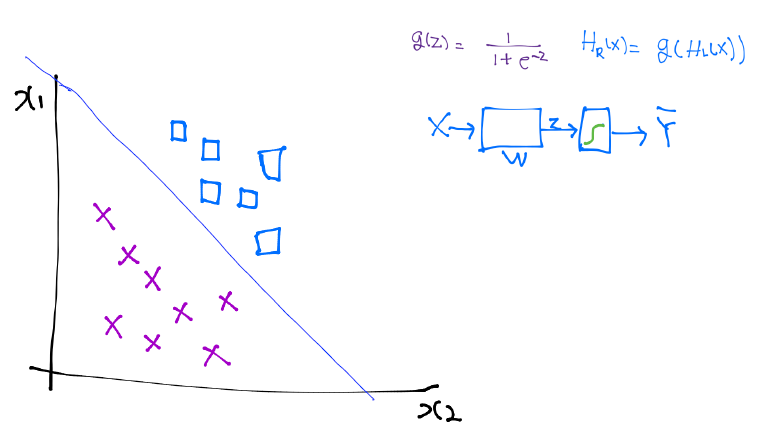
x1, x2의 값을 가지고 있고, 분류해야 할 데이터들이 네모와 엑스 표가 있는 데이터라고 하자.
W를 학습한다 (= logistic classification을 학습한다)는 것이 무엇인가?
--> 두 개를 구분하는 선을 찾아내는 것! (hypo-plain: 여러 차원에서)
Multinomial classification (에 적용)
: 여러 개의 class가 있다는 뜻

데이터가 표처럼 주어졌다고 가정.
y값으로 학점을 준다고 하자. (A, B, C 3가지)
대략 그래프로 표시한 것이 오른쪽 그래프.

- Binary Classification만을 가지고 Multinomial classification 구현이 가능하다!
ex) 하나의 classfication을 만들어 (1)과 같은 hypo-plain을 찾아냈다.
이것은 무조건 C거나 C가 아니거나 둘 중 하나만을 보는 것 --> binary classification
(2) = B or not
(3) = A or not
--> 3개의 각기 다른 binary classification을 가지고 충분히 구현 가능하다.

- 각각 하나의 classification에 대해서 보자.
: 구현할 때는 matrix(행렬)로 구현!

세 번 독립된 형태의 vector를 가지고 계산
--> 독립적으로 각각 계산하면 복잡하고 번거로울것!
한번에 계산하기 위하여 W를 다음과 같이 밑으로 늘인다고 가정해보자.

--> 하나의 vector로 이렇게 처리하면 한번에 계산 가능하고 독립된 classification들처럼 간단하게 될 수 있다.
Where is sigmoid?
Ha(x), Hb(x), Hc(x) 각각에 sigmoid를 적용하여도 되지만 이것을 효율적으로 간단히 하는 방법을 다음에 배울 것.
'인공지능' 카테고리의 다른 글
| [모두의 딥러닝] lab 06-1. TensorFlow로 Softmax Classification 구현하기 (1) | 2019.04.10 |
|---|---|
| [모두의 딥러닝] lec 06-2. Softmax classifier의 cost 함수 (0) | 2019.04.08 |
| [모두의 딥러닝] lab 05. TensorFlow로 Logistic Classification 구현 (0) | 2019.04.08 |
| [모두의 딥러닝] lec 05-2. Logistic Regression의 cost 함수 설명 (0) | 2019.04.08 |
| [모두의 딥러닝] Logistic Classification의 가설 함수 정의 (0) | 2019.04.07 |


댓글