[모두의 딥러닝] lec 05-2. Logistic Regression의 cost 함수 설명
Cost function

가설로 예측한 값과 실제 값의 차이를 제곱한 것.
장점) 어디에서 시작하든 최저값을 찾을 수 있는 그래프
이전 가설

일차방정식 선의 제곱 때문에 매끄럽게 구부러지는 그래프가 만들어짐.
따라서 어느 지점이든 최저점에 도달 가능
바뀐 가설
: 출력값이 항상 0~1 사이에 들어오도록 만듦.

이제는 linear한 그래프가 아님. g(z)의 선(오른쪽 위)이 제곱되었기 때문에
다음과 같은 그래프가 만들어짐.
문제점)
gradient desent를 적용하면 시작점이 어디냐에 따라 끝나는 점이 달라질 수 있음.
ex. 기울기가 없는 곳이라면 최저점이라고 생각할 것임.
Local minimum
Global minimum: 우리가 찾고자 하는 전체 최저점
g.m을 찾고자 하는 것이 목표였지만 l.m에서 학습이 멈춰버릴 수 있다.
--> 모델이 굉장히 나쁘게 예측할 수 있음.
--> 사용 불가능
==> cost 함수의 형태를 좀 바꾸자!
New COST FUNCTION for logistic
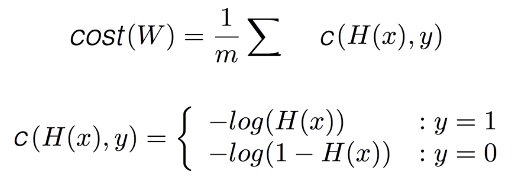
c(H(x), y) 함수 --> 두 가지 경우로 정의된다.
두 가지로 나누어 함수가 정의되는 이유?
understanding cost function

e^-z이 들어가 있기 때문에 구부러진 것처럼 만들어낸다.
이것과 상극이 되는 것은 log함수.
log함수를 사용하는 것이 기본 아이디어
(y = 학습으로 주어진 data label)
<y=1: C(H(x), y) = -log(H(x))>

z값이 1이면 함수의 값은 0이 된다.
z값이 0에 가까워지면 함수의 값은 커진다.
cost 함수 = 실제 값과 예측한 값이 비슷하면 값 작아지고, 차이나면 값 커진다.
--> cost를 최소화하기 위하여 weight 변경하는 것임.
y=1일때 H(x)=1로 맞은 경우? --> cost(1) = 0
y=1일때 H(x)=0으로 예측이 틀린 경우? --> cost(0) = 무한대
==> 예측이 틀리면 cost가 굉장히 높아져서 시스템에 벌을 준다.
<y=0: C(H(x), y) = -log(1-H(x))>

y=0일때 H(x)=0으로 예측이 맞은 경우? --> cost(0) = 0
y=0일때 H(x)=1로 예측 실패한 경우? --> cost(1) = 무한대
==> 예측을 잘못했을 경우 cost 값을 크게 한다.
결론: 원래 cost함수의 목적과 잘 맞음.
이 두 그래프를 붙이면 우리가 원했던 밥그릇 모양이 나오는 것임.
--> Gradient decent 알고리즘 적용 가능.
Cost function 결론
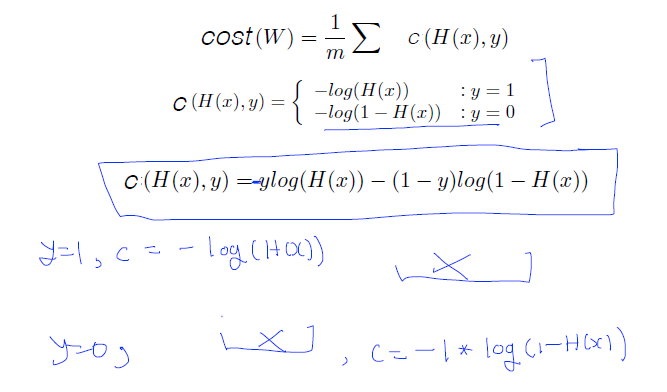
tensorflow에서 직접 함수를 돌리다보면 복잡할 것임. (이유: 조건문)
--> if condition을 없애보자고 만든 함수!
Minimize cost - Gradient decent 알고리즘
cost함수를 최소화하는 방법인 경사타고 내려가기 알고리즘을 적용하자!

미분을 하는 것은 컴퓨터의 도움을 받자.
내려가는 한 발자국의 값을 알파로 주고, 그 값의 결과에 따라 알파의 값을 update 시키면 된다.

W의 부분은 GradientDescentOptimizer라는 라이브러리를 이용하여 사용하면 된다.
'인공지능' 카테고리의 다른 글
| [모두의 딥러닝] lec 06-1. Softmax Regression: 기본 개념 소개 (0) | 2019.04.08 |
|---|---|
| [모두의 딥러닝] lab 05. TensorFlow로 Logistic Classification 구현 (0) | 2019.04.08 |
| [모두의 딥러닝] Logistic Classification의 가설 함수 정의 (0) | 2019.04.07 |
| [모두의 딥러닝] lab 04-2. Loading Data from File (0) | 2019.04.06 |
| [모두의 딥러닝] lab 04-1. multi-variable linear regression을 TensorFlow에서 구현하기 (0) | 2019.04.05 |


댓글