[모두의 딥러닝] Logistic Classification의 가설 함수 정의
Logistic Classification
- Classification 알고리즘 중 정확도가 높은 알고리즘
- 실제 문제에도 적용 가능
- neural network과 deep learning의 중요한 구성 요소
Linear Regression 복습
HCG
- Hypothesis

- Cost 함수

가설과 실제 값의 차이를 평균 낸 것
데이터를 이용하여 cost를 최소화하는 weight를 찾는 것.
- Gradient decent
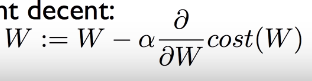
경사 타고 내려가기 알고리즘
어떤 지점에서 시작하든 기울기를 본 후 한 발자국 움직여서 최저점을 찾을 수 있는 것.
기울기 = cost함수를 미분한 값
알파 값 = 한 번에 움직이는 step size = learninng rate
(Binary) Classification (중요)
- 이전까지는 숫자를 그냥 예측하는 것이었음.
- 둘 중 하나, 즉 정해진 카테고리 내에서 고르는 것
- Spam (Email) Detection: Spam(1) or Ham(0)?
- Facebook feed: show(1) or hide(0)?
친구들이 만들어낸 무수한 타임라인에서 내가 좋아요 누른 것을 학습하여 좋은 것들만 보여준다.
- Credit Card Fraudulent Transaction detection: legimate(0)/fraud(1)
분실된 신용카드
이전에 쓰던 소비패턴을 학습하여 가짜를 판별
- 머신러닝에서 많이 활용되는 분야.
--> 기계적인 학습을 위하여 0, 1로 encoding
- 사용 예시
1. Radiology
이미지를 보고 이것이 나쁜 tumor인지 좋은 것인지
2. Finance
이 주식을 살 것인지 팔 것인지 이전 시장 동향을 학습하여 판단
사람보다 더 잘하는 분야
- 예시
Pass(1)/Fail(0) based on study hours BY Linear Regression

이 모델의 문제점 1)
ex) 50시간을 공부하면 linear regression에서는 큰 값이 나올 것.
하지만 이 모델에서는 1(pass)의 값만 가질 것.
학습시키면 선이 기울어질 것인데, 0.5와 비교했을 때 합격/불합격 기준선이 달라질 것임.
이 모델의 문제점 2)

x가 엄청 큰 수라면 1을 훨씬 뛰어 넘는 값이 나올 것.
결론
Linear Regression이 간단하고 좋기는 하지만 0~1 사이의 값으로 함축할 수 있는 함수를 찾고 싶다!
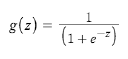
sigmoid function = logistic function
: curved in two directions, like the letter "S" or the Greek sigma

이 함수는 값이 커져도 1로 수렴하고 값이 작아져도 0으로 수렴
z = wx
H(x) = g(z)
대입해보면
Logistic Hypothesis 가설 함수

'인공지능' 카테고리의 다른 글
| [모두의 딥러닝] lab 05. TensorFlow로 Logistic Classification 구현 (0) | 2019.04.08 |
|---|---|
| [모두의 딥러닝] lec 05-2. Logistic Regression의 cost 함수 설명 (0) | 2019.04.08 |
| [모두의 딥러닝] lab 04-2. Loading Data from File (0) | 2019.04.06 |
| [모두의 딥러닝] lab 04-1. multi-variable linear regression을 TensorFlow에서 구현하기 (0) | 2019.04.05 |
| [모두의 딥러닝] lec 04. multi-variable linear regression (0) | 2019.04.04 |


댓글